가속도 센서 하나만으로 방향을 계산할 수 있을까? 최근 프로젝트로 가속도계를 사용하게 되었는데 요구사항이 많아서, 가속도계의 기본 원리부터 여러가지를 공부하였다. 또한 정확한 방향 계산을 위해 왜 다른 센서들이 필요한지도 알게 되었다. 이 글에서는 Pitch, Roll, Yaw라는 방향의 3요소를 이해하고, 가속도 센서와 자이로 센서를 이용해 방향을 계산하는 실제 코드까지 살펴보기로 하자.
리스트
모든 것의 시작, 가속도 센서
방향 계산의 가장 기본이 되는 센서는 바로 가속도 센서(Accelerometer)다. 이름 때문에 움직일 때만 쓰는 센서라고 오해하기 쉽지만, 이 센서의 진짜 능력은 중력을 감지하는 것이다.
정지 상태의 가속도 센서는 항상 지구 중심 방향으로 작용하는 중력을 측정한다. 센서가 수평일 때와 기울어졌을 때, 이 중력이 각 축(X, Y, Z)에 나뉘어 측정되는 값의 차이를 이용하면 현재 센서의 정적인 기울기를 알아낼 수 있다.
가속도 센서의 한계와 다른 센서들의 역할
하지만 가속도 센서만으로는 완전한 방향 계산이 불가능하다. 그 이유는 다음과 같다.
- 한계 1: 회전을 모른다.
가속도 센서는 현재 기울어진 ‘상태’만 알 수 있다. 팽이처럼 제자리에서 빙글빙글 도는 ‘회전’ 움직임은 감지하지 못한다. 이 역할을 해주는 것이 바로 자이로 센서(Gyroscope)다. 자이로는 물체의 회전 속도(각속도)를 측정해 동적인 움직임을 파악하게 해준다. 6축 센서에 있다. - 한계 2: 절대 방향을 모른다.
가속도 센서는 동서남북과 같은 절대적인 방향을 알지 못한다. 이 역할을 하는 것이 지자기 센서(Magnetometer)다. 지자기 센서는 지구 자기장을 감지해 나침반처럼 북쪽이 어디인지를 알려주어 절대적인 방향 기준을 잡아준다. 지자기 센서를 사용하기 위해서는 9축 센서를 사용해야 한다.
보통 이 세 가지 센서를 조합해 3축(가속도), 6축(가속도+자이로), 9축(가속도+자이로+지자기) 센서라고 부른다.
움직임의 3요소: Pitch, Roll, Yaw
물체의 3차원 방향은 보통 세 가지 각도로 표현한다. 비행기 움직임을 생각하면 아주 쉽다.
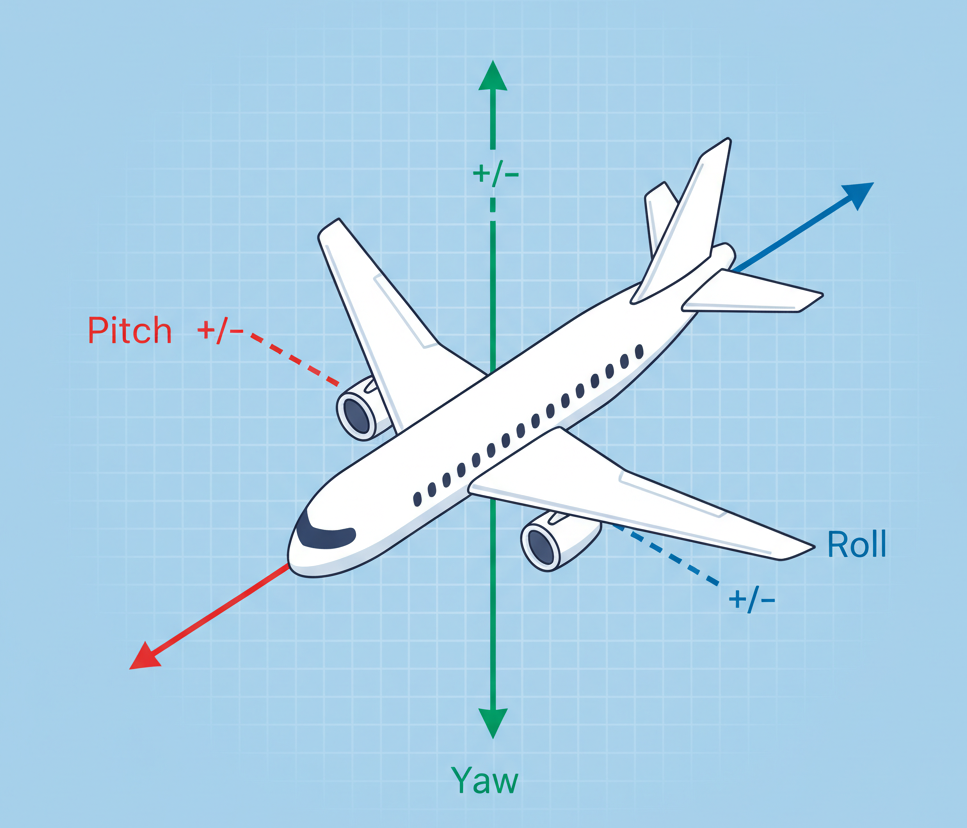
- Pitch (피치): 비행기의 앞머리가 위아래로 움직이는 것. (끄덕끄덕 하는 모양)
- Roll (롤): 비행기의 날개가 좌우로 기울어지는 것. (고개 갸웃갸웃 하는 모양)
- Yaw (요): 비행기의 기수가 수평면에서 좌우로 방향을 트는 것. (고개를 도리도리 하는 모양)
이 세 가지 각도만 알면 3차원 공간에서 물체가 어떤 자세를 하고 있는지 정확히 알 수 있다. Roll과 Pitch는 가속도 센서로 계산이 가능하지만, Yaw는 지자기 센서가 있어야 정확한 값을 계산할 수 있다.
가속도 센서만으로는 Yaw 계산이 불가능 하다. Yaw는 중력 방향(수직축)을 기준으로 수평면에서 회전하는 각도다. 가속도 센서는 중력 방향만을 기준으로 하므로, 물체가 제자리에서 수평으로 아무리 회전해도 가속도 센서 값은 변하지 않는다.
센서 값 읽기: ‘g’ 단위의 이해
가속도계를 사용하여 방향 벡터 값을 계산하려면, 먼저 가속도계의 세 축(x, y, z)을 따라 가속도 값을 측정해야 한다.
이 값들은 보통 ‘g’ 라는 단위로 나오는데, 이것은 **중력 가속도(Gravity)**를 기준으로 한 값이다. 1g는 약 9.8m/s²를 의미한다. 즉, 센서가 Z축으로 -1.0이라는 값을 출력한다면, 그건 아래 방향으로 9.8m/s²의 중력 가속도를 온전히 받고 있다는 뜻이다.
센서를 수평으로 가만히 두면 보통 이런 식으로 Z축에만 중력 가속도 값이 실리고, X와 Y축은 0에 가까운 값이 나온다.
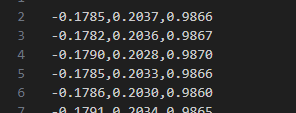
이 상태에서 센서를 기울이면 중력 값이 각 축으로 분산되면서 X, Y, Z 값이 바뀌게 되고, 우리는 바로 이 값들을 이용해 기울기를 계산하는 것이다.
코드로 보는 방향 계산의 기초
이제 개념을 알았으니 실제 코드로 만들어 보자. 아래는 센서 값을 읽어왔다는 가정하에 각 항목을 계산하는 공식과 C언어 코드 예제다.
1. 가속도 센서로 정적 기울기(Pitch, Roll) 구하기
다음 공식은 정지 상태에서 중력을 이용해 현재 기울기를 계산하는 방법이다.
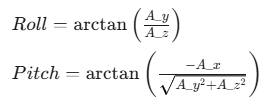
그리고 소스코드는 다음과 같다.
#include <math.h>
// 센서 값 구조체 (예시)
typedef struct {
float accel_x, accel_y, accel_z;
float gyro_x, gyro_y, gyro_z;
} ImuData;
// 각도를 담을 구조체 (예시)
typedef struct {
float pitch, roll, yaw;
} Angles;
// 라디안을 각도로 변환하는 매크로
#define RAD_TO_DEG(rad) ((rad) * 180.0 / M_PI)
/**
* @brief 가속도 센서 값으로 기울기(Pitch, Roll)를 계산한다.
* @param imu_data 센서 데이터 포인터
* @param angles 계산된 각도를 저장할 포인터
*/
void calculate_tilt(const ImuData* imu_data, Angles* angles) {
float ax = imu_data->accel_x;
float ay = imu_data->accel_y;
float az = imu_data->accel_z;
// Roll 계산 (Y축, Z축 사용)
angles->roll = RAD_TO_DEG(atan2(ay, az));
// Pitch 계산 (X축, Y축, Z축 사용)
angles->pitch = RAD_TO_DEG(atan2(-ax, sqrt(ay * ay + az * az)));
}2. 자이로 센서로 각도 변화량 구하기
자이로 센서로 회전 속도를 측정해 시간에 따라 각도가 얼마나 변했는지 계산하는 방법이다.
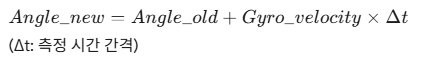
이것을 코드로 작성하면 다음과 같다.
// 이전 측정 시간을 저장할 변수 (static 또는 전역)
static unsigned long last_time = 0;
/**
* @brief 자이로 센서 값으로 각도의 변화를 누적 계산한다.
* @param imu_data 센서 데이터 포인터
* @param angles 이전 각도 값이자, 새로운 각도를 저장할 포인터
*/
void update_orientation(const ImuData* imu_data, Angles* angles) {
unsigned long current_time = millis(); // 현재 시간 (ms)
if (last_time == 0) {
last_time = current_time;
return;
}
// 시간 변화량 계산 (초 단위)
float dt = (current_time - last_time) / 1000.0f;
last_time = current_time;
// 각 축의 각속도(degree/s)를 이용해 각도 변화 누적
angles->roll += imu_data->gyro_y * dt;
angles->pitch += imu_data->gyro_x * dt;
angles->yaw += imu_data->gyro_z * dt;
}주의할 점은, 자이로 센서만 사용하면 시간이 지날수록 오차가 계속 쌓인다는 것이다. 이것을 Drift 현상 이라고 한다. 그래서 실제로는 가속도 센서 값으로 이 오차를 보정해주는 과정이 필요하다. 오차를 보정해 주는 것에 여러가지 필터를 사용한다고 한다. 실제 상용 제품에서는 가속도계로 기울기를 보정해주는 상보 필터나 칼만 필터를 사용한다.
센서 데이터를 이해하면 길이 보인다
가속도 센서 하나로 시작했던 방향 계산은 3축, 6축, 9축 센서의 차이점을 이해하고, Pitch, Roll, Yaw라는 움직임의 핵심 개념을 파악하는 과정으로 이어졌다. 그리고 가속도 센서가 정적인 기울기를, 자이로 센서가 각도의 변화를 알려준다는 것도 실제 코드 예제를 통해 직접 확인하였다.
센서 데이터는 처음 보면 그저 복잡한 숫자들의 나열처럼 보일 수 있다. 하지만 이 값들이 중력, 회전, 자기장이라는 물리적 현상을 어떻게 반영하는지 그 원리를 이해하고 나면, 모든 데이터가 의미 있는 정보로 바뀌게 된다. 이 글에서 다룬 기본적인 계산 방법과 코드 예제는 더 복잡한 센서 퓨전 알고리즘이나 실제 애플리케이션 개발로 나아가는 튼튼한 첫걸음이 될 것이다.

